108. Максимальная
сумма
Имеется таблица ![]() , состоящая из целых чисел. Необходимо найти в ней
прямоугольник с максимальной суммой. Например, в таблице
, состоящая из целых чисел. Необходимо найти в ней
прямоугольник с максимальной суммой. Например, в таблице
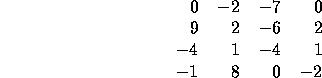
прямоугольником с наибольшей суммой будет

Сумма его элементов равна
15.
Вход. Первым является число n – размер таблицы.
Далее следуют n2 чисел, непосредственно описывающие саму таблицу. Известно,
что n £ 100, все числа
в таблице находятся в промежутке [-127, 127].
Выход. Значение
суммы в максимальном прямоугольнике.
Пример входа
4
0 -2 -7 0 9 2 -6 2
-4 1 -4 1 -1
8 0 -2
Пример выхода
15
РЕШЕНИЕ
динамическое программирование
Анализ алгоритма
Пусть входная таблица
хранится в массиве table, причем верхняя левая
ячейка таблицы хранится в table[1][1].
Пересчитаем ее элементы таким образом, чтобы _table[i][j]
= ![]() . То есть _table[i][j] содержит сумму элементов table[i][j] которые находятся в той же
колонке, но не ниже элемента (i, j).
. То есть _table[i][j] содержит сумму элементов table[i][j] которые находятся в той же
колонке, но не ниже элемента (i, j).
Теперь сумму чисел s любого прямоугольника с левым верхним углом (i1, j1) и правым нижним (i2, j2) можно вычислить за
линейное время:
s = ![]()
Слева представлена входная
таблица table, справа – преобразованная.
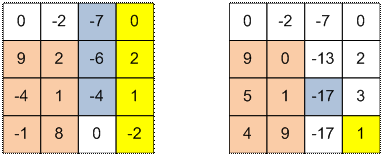
Например
_table[3][3] = table[1][3] + table[2][3] + table[3][3] = -7 – 6 – 4 = -17,
_table[4][4] = table[1][4] + table[2][4] + table[3][4] + table[4][4] = 0 + 2 + 1 – 2 = 1
Сумма чисел в
прямоугольнике (2, 1) – (4, 2) равна
![]() =
=
![]() = (4 – 0) + (9 – (-2)) = 15
= (4 – 0) + (9 – (-2)) = 15
Зафиксируем две строки i и j. Найдем величину максимального прямоугольника, упирающегося
сверху в строку i, а снизу в строку j (обе строки включительно). Построим последовательность
А чисел a1, a2, …, an, для которой ak = _table[j][k] – _table[i – 1][k]. Остается найти такую подпоследовательность подряд идущих чисел в последовательности А, которая имеет максимально возможную сумму. Это известная одномерная
задача, которая решается через частичные суммы sk = a1 + … + ak (как только частичная
сумма становится меньше 0, мы ее обнуляем и считаем дальше).
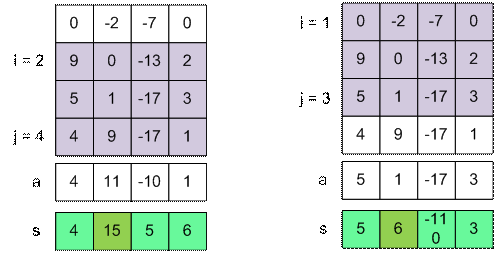
Максимальный прямоугольник
между:
·
строками 2 и 4 имеет сумму 15;
·
строками 1 и 3 имеет сумму 6;
Реализация алгоритма
Объявим макросы глобальный массив.
#define MAX 102
int table[MAX][MAX];
Читаем входные данные.
scanf("%d",
&n);
memset(table,0,sizeof(table));
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
scanf("%d",&table[i][j]);
Пересчитываем массив
table.
for (j = 1; j <= n; j++)
for (i = 1; i <= n; i++)
table[i][j] = table[i
- 1][j] + table[i][j];
Ищем прямоугольник с
максимальной суммой. Перебираем строки i и j (1 ≤ i ≤ j ≤ n). Далее считаем частичные суммы sk и решаем одномерную задачу.
for (i = 1; i <= n; i++)
for (j = i; j <= n; j++)
{
t = 0;
for (k = 1; k <= n; k++)
{
t += table[j][k] - table[i-1][k];
if (t < 0)
t = 0;
if (t >
max) max = t;
}
}
Выводим сумму в
максимальном прямоугольнике.
printf("%d\n",
max);